Introduction of Two-Phase Flow
Multiphase Flow
다상유동 (multiphase)은 기체, 액체 및 고체상들이 혼합되어 있는 유동을 의미한다. 다상유동은 점도, 밀도 등 물성치가 다른 2개 이상의 유체가 혼합되어 있기 때문에 각 상간의 상호작용으로 인해 단상유동과는 다른 유동현상이 나타난다.
Two-Phase Flow
고체 혼합물과는 달리 (고체 형상이 녹거나 어는 경우를 제외하고), 기체-액체 2상 유동 (gas-liquid two-phase flow)에서는 상 경계면이 지속적으로 변하고, 각 상 내부의 유동이 존재하기 때문에 복잡하다. 또한 이러한 기체-액체 2상 유동은 상변화 열전달 (phase change heat transfer)현상과 연관되어 있다.
비록 엄밀하게는, 2상 유동은 수증기-물과 같이 동일한 화학적 성분을 가진 물질이 서로 다른 상으로 공존하는 유동을 의미하고, 공기-물과 같이 2개의 서로 다른 화학성분으로 구성된 유동은 2성분 유동 (two component flow)이지만, 두 유동은 제반현상뿐만 아니라, 해석 및 실험 방법면에서도 많은 유사성이 있기 때문에 모두 2상유동이라고 칭하고 있다.
2상유동의 연구방법은 다음과 같이 정리될 수 있다.
- 실험을 통하여 correlation을 얻는 방법
- 대형장치내의 2상 유동을 실험실 규모의 장치에서 예측할 수 있도록 모사하는 scaling law가 필요
- Differential analysis
- 미소체적에 대한 balance equation으로부터 conservation equation을 얻고, 이를 풀어서 각 상의 속도, 온도, 농도 분포등을 예측
- 보존방정식을 푸는 데 필수적인 constitutive relations (e.g., 각 상의 상호작용에 의한 난류현상의 변화를 고려한 각 상의 난류 모델, 상 경계면 형상 및 면적의 변화에 대한 모델) 필요
- Integral analysis
- 속도, 온도에 대해 적절한 분포함수 형태를 가정하고, 관심있는 유동영역에서 전반적인 보존관계를 만족시킬 수 있는 분포함수의 변수를 결정
- 적당한 분포함수의 가정을 위해서는 유동의 물리적 현상 파악이 필요
- Flow pattern에 관계없이 간단한 거시적 모델을 세워 유동을 기술하는 방법 (e.g., homogeneous mixture model)
Basic Flow Patterns
2상 유동은 다양한 flow pattern을 지니고 있다 (e.g., 액체 내의 기포, 기체 내에 액적, 그리고 상부의 기체와 하부의 액체가 흐르는 유동). 열전달이나 물질전달 (condensation과 evaporation)의 정도는 flow pattern에 따라 크게 좌우된다.
기체와 액체는 밀도차가 크기 때문에 기체는 부력을 받아 중력과 반대 방향으로 항상 떠오른다. 따라서, 유동방향이 수직 또는 수평에 따라 flow pattern도 변한다.
Vertical Flows
Vertical flow의 경우, 중력이 유동 방향과 같거나 정반대이므로 유동의 형태가 축대칭이다. Vertical flow pattern은 bubbly flow, slug flow, churn flow, annular flow, and drop flow 등이 있다. 각 flow pattern의 경계가 명확히 구분되지는 않고, 천이할 때는 2개의 pattern이 섞여서 나타난다.
Bubbly flow
liquid phase 내에 gas phase가 분산된 작은 기포의 축대칭 형태로 분포한다. 기포의 직경은 관 직경에 비해 매우 작기 때문에 관 벽면으로부터 직접적인 영향을 받지 않고, 간접적으로 영향을 받는다 (i.e., 관 벽에 접촉하고 있는 liquid phase에 의해 기포의 유동이 영향을 받는다). void fraction (단위 체적당 기체가 차지하는 체적의 비)가 0.3 이하에서 주로 나타난다.
Slug flow
관 직경과 거의 같은 직경을 가지는 Taylor bubble이 상향으로 흐르고, Taylor bubble과 벽면 사이에서는 액체가 얇은 film의 형태로 하향 유동을 한다. bubbly flow가 하류로 흘러가면서 작은 기포들 간의 합착에 의해서 형성된다.
Churn flow
앞부분이 둥근 형태의 slug flow와는 달리 기포의 형태가 많이 변형되어 불규칙적인 형태를 이루며, liquid slug가 기체 유동에 의해 파괴되었다가 복원됨에 따라 유동 전체가 oscillation을 한다. 이에 따라.
Annular flow
liquid는 벽을 따라 film의 형태로 흐르고, gas는 중심부를 따라 흐른다. 기체의 흐름이 클 때 일반적으로 나타나며, liquid film으로 부터 작은 liquid drop이 떨어져 나와 기체 유동에 entrainment되는 경우가 많다 (annular-mist flow).
Drop flow
liquid가 drop의 상태로 기체유동에 실려서 흘러가는 유동으로, 액체유량에 비해 기체유량이 매우 클때 나타나며 dispersed flow, mist flow, 또는 spray flow로도 언급된다.
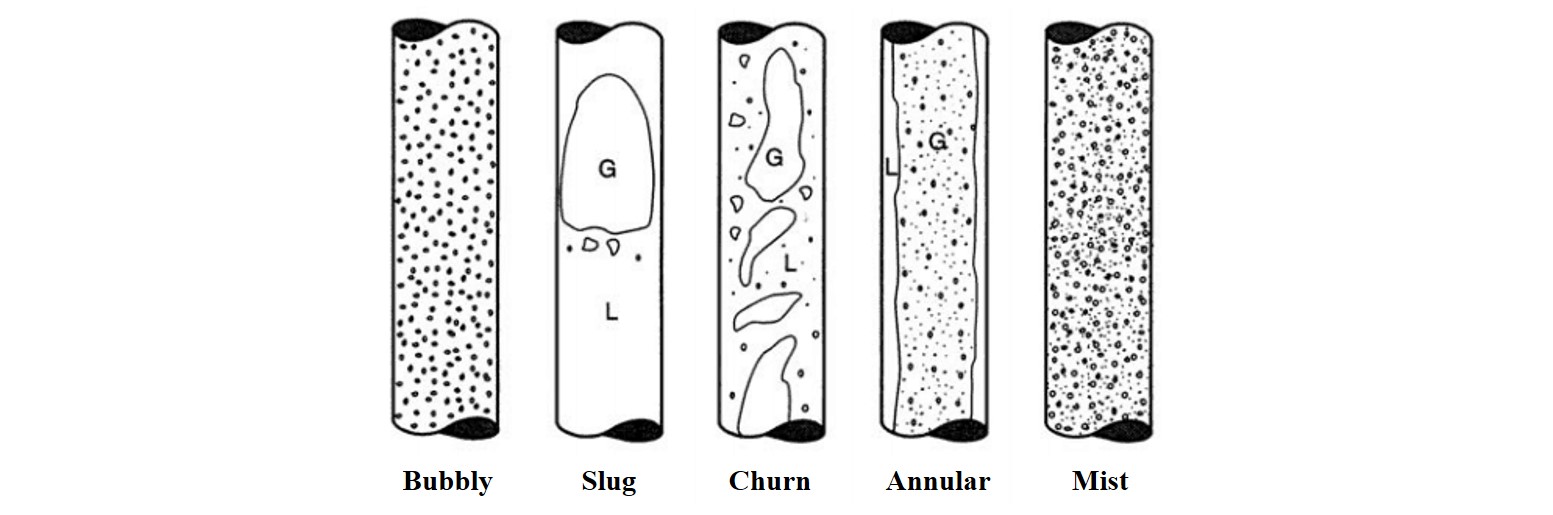
(taken from Handbook of fluids in motion by Cheremisinoff, N. P., & Gupta, R.)
heat transfer가 수반되지 않는 유동 (엄밀하게, two-component flow)의 경우는 flow pattern이 그대로 유지되지만, heat transfer가 수반 되는 evaporative flow나 condensing flow의 경우에는 유동방향에 따라 flow pattern이 크게 변하게 된다.
Horizontal Flows
Horizontal flow의 경우, 중력이 반경 방향으로 작용하므로 유동이 중심축에 대해 비대칭 형태를 가지며, 밀도가 큰 액체는 아래쪽에서 흐르는 경향을 보인다. Horizontal flow pattern은 bubbly flow, plug flow (elongated bubbly flow), stratified flow, wavy flow, slug flow, and annular flow 등이 있다.
Bubbly flow
Liquid phase에 작은 기포가 분산된 형태이다. 부력에 의해 기포들은 상부에 더 많이 분포하여 흐른다.
Plug flow
Bubbly flow가 느려지면 기포들 간의 합착에 의해 긴 형태의 bubble이 형성되며,상부를 따라서 흐른다.
Stratified flow
기체와 액체가 모두 느린 속도로 흐를때 나타나며, 기체와 액체간 상대 속도가 작기 때문에 두 유체간의 interface는 smooth한 형태를 가진다.
Wavy flow
Stratified flow에서 기체의 속도가 증가하게 되면, 두 유체간의 상대 속도가 커지게 되면서 interface가 교란을 받아 surface wave가 발생하는 유동이다. surface wave는 유동 방향으로 움직인다.
Slug flow
Plug flow와 외형상 비슷하나, 빠른 속도의 기체의 의해서 발생한다.
Annular flow
빠른 속도의 기체가 중심 부분을 흐르고, 상대적으로 느린 액체는 벽을 따라서 film의 형태를 가지고 같은 방향으로 흐른다. 중력에 의해 상부는 항상 liquid film으로 덮여있진 않고, 하부에서는 좀 더 두꺼운 liquid film을 형성한다. 속도가 증가하면, liquid film으로부터 liquid drop이 기체 유동에 유입된다 (annular-mist flow).
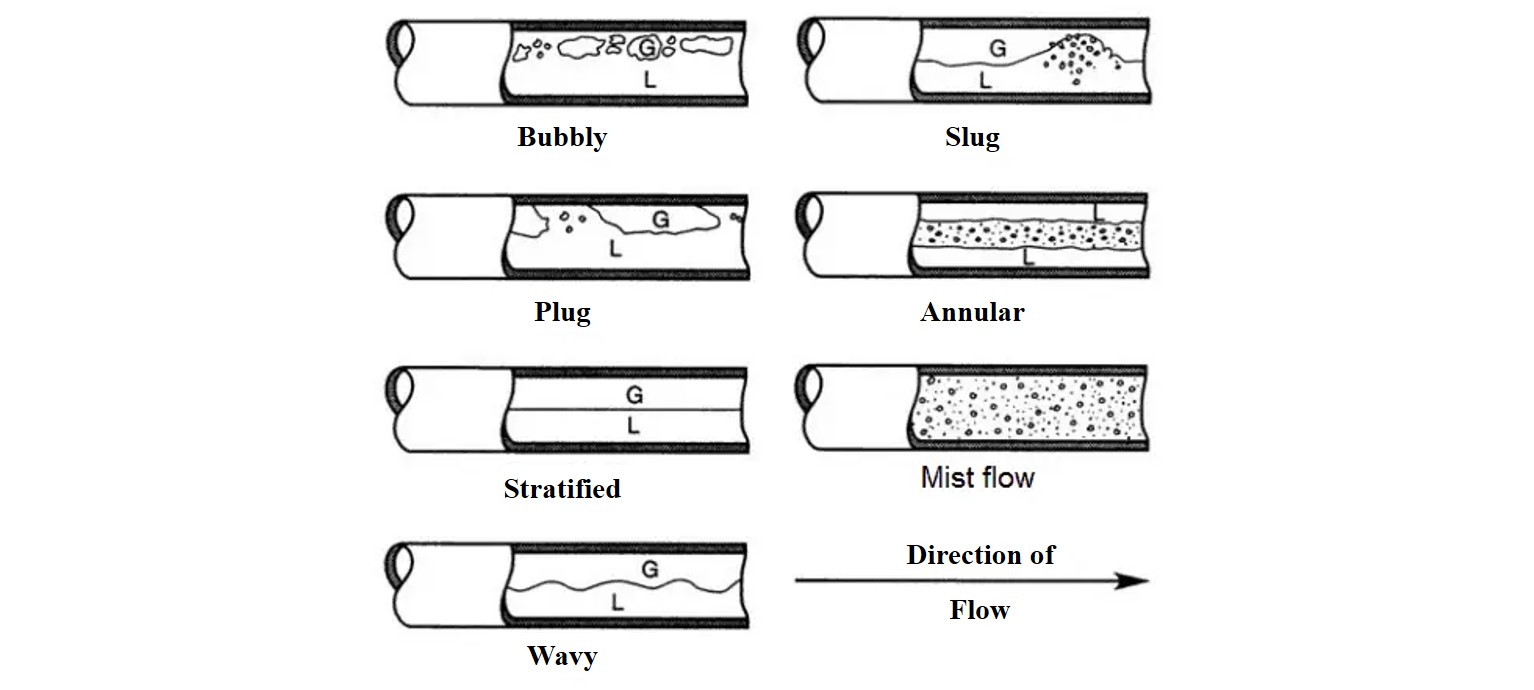
(taken from Handbook of fluids in motion by Cheremisinoff, N. P., & Gupta, R.)
Notations and Relations
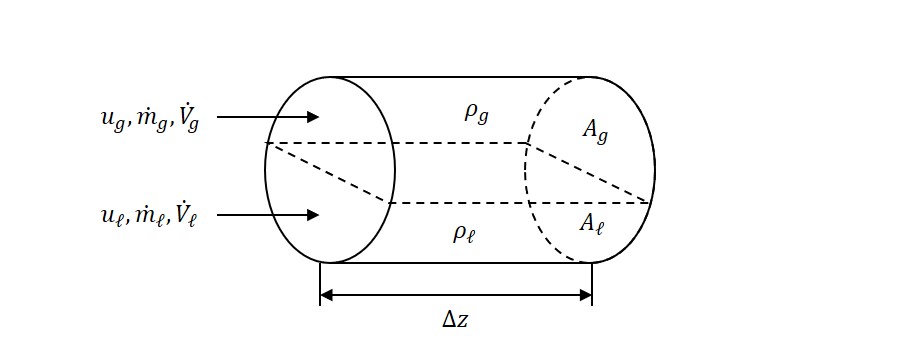
각 phase의 속도와 유량등 여러 변수들 간의 관계를 정의하기 위해, 위의 그림에서 보는 것처럼, 유동 단면적 \(A\)를 밀도가 \(\rho_{\ell}\)인 액체와 \(\rho_{g}\)인 기체가 각각 속도 \(u_{\ell}\)와 \(u_{g}\)로 함께 흐르는 1차원 유동을 생각할 수 있다. 각 상이 차지하는 유동 단면적을 각각 \(A_{\ell}, A_{g}\)라고 하면 다음과 같이 표현할 수 있다.
\[A=A_{\ell}+A_{g}\]여기서, 아래와 같이 기체가 차지하는 체적 \((A_{g}\cdot\Delta z)\)을 전체 체적 \((A\cdot\Delta z)\)으로 나누면 void fraction \((\alpha)\)을 구할 수 있다.
\[\alpha = A_{g}/A\] \[1-\alpha = A_{\ell}/A\]기체와 액체의 mass flow rate \((\dot{m})\)은 각각 아래와 같으며,
\[\dot{m_g}=u_{g}\rho_{g}A_{g}\] \[\dot{m_\ell}=u_{\ell}\rho_{\ell}A_{\ell}\]Total mass flow rate은 다음과 같다.
\[\dot{m}=\dot{m_g}+\dot{m_\ell}\]기체와 액체에 대한 volume flow rate \((\dot{V})\)은 각각 아래와 같으며,
\[\dot{V_g}=u_{g}A_{g}=\dot{m_g}/\rho_{g}\] \[\dot{V_\ell}=u_{\ell}A_{\ell}=\dot{m_\ell}/\rho_{\ell}\]Total volume flow rate은 다음과 같다.
\[\dot{V}=\dot{V_g}+\dot{V_\ell}\]Total mass flow rate에 대한 기체 mass flow rate의 비를 quality 또는 mass quality \((x)\)라고 부르며, 아래와 같이 표현한다.
\[x=\dot{m_g}/\dot{m}\] \[1-x=\dot{m_\ell}/\dot{m}\]단위 면적당 mass flow rate인 mass flux \((J)\)는 아래와 같은 relation을 가진다.
\[J_{\ell} = \dot{m_\ell}/A\] \[J_{g} = \dot{m_g}/A\] \[J = \dot{m}/A = J_{\ell} + J_{g}\]단위 면적당 volume flow rate인 superficial velocity \((S)\)는 아래와 같은 relation을 가진다.
\[S_\ell=\dot{V_\ell}/A\] \[S_g=\dot{V_g}/A\] \[S = \dot{V}/A =S_\ell + S_g\]total volume flow rate에 대한 기체 volume flow rate의 비를 volume quality \((\beta)\)라고 정의하며, 아래와 같다.
\[\beta = \dot{V_g}/\dot{V}\] \[1-\beta = \dot{V_\ell}/\dot{V}\]앞서 정의한 void fraction \((\alpha)\), mass flow rate \((\dot{m})\), mass flux \((J)\), volume flow rate \((\dot{V})\), superficial velocity \((S)\), mass quality \((x)\), volume quality \((\beta)\)와 기체 및 액체의 실제 속도 \((u_g, u_\ell)\)간의 관계식을 정리하면 다음과 같다.
\[u_g = \dot{m_g}/\rho_{g}A_g = \dot{V_g}/A_g=Jx/\alpha\rho_g\] \[u_\ell = \dot{m_\ell}/\rho_\ell A_\ell=\dot{V_\ell}/A_\ell=J(1-x)/(1-\alpha)\rho_\ell\] \[S_g=u_g\alpha=S\beta=Jx/\rho_g\] \[S_\ell=u_\ell(1-\alpha)=S(1-\beta)=J(1-x)/\rho_\ell\] \[\frac{u_g}{u_\ell}=\frac{x}{1-x}\frac{\rho_\ell}{\rho_g}\frac{1-\alpha}{\alpha}\]기체와 액체간의 relative velocity는 아래와 같으며,
\[u_{g,\ell}=u_g - u_\ell\] \[u_{\ell, g} = u_\ell - u_g\]기체 (또는 액체)속도와 superficial velocity와의 relative velocity인 drift velocity는 다음과 같다.
\[u_{g, \text{s}}=u_g - S\] \[u_{\ell, \text{s}}=u_\ell - S\]drift flux (평균 속도에 대한 각 phase의 superficial velocity)는 아래와 같은 relation을 가진다.
\[S_{g, \ell}=\alpha(u_g - S)=\alpha u_{g,s}\] \[S_{\ell, g}=(1-\alpha)(u_\ell-S)=(1-\alpha)u_{\ell,s}\] \[S_{g, \ell} = -S_{\ell, g}\] \[S_{g, \ell} = (1-\alpha)S_g - \alpha S_\ell\] \[S_{\ell, g} = \alpha S_\ell - (1-\alpha)S_g\] \[S_{g,\ell} = \alpha(1-\alpha)u_{g, \ell}\]Flow Patterns Maps
Flow patterns maps을 통해 다양한 flow pattern를 2차원 상에서 표현할 수 있지만, flow pattern 변화는 많은 변수들에 의존하기 때문에 2차원 상에서 모든 flow pattern을 완전히 표현할 수는 없다. 따라서 각 maps을 상황에 맞게 적용해야 한다.